WEB APP FREE
GRATIS al 100%

Calcolatore Area
Calcola l’area delle principali figure geometriche
Area quadrato – Area rettangolo – Area triangolo
Area trapezio – Area rombo – Area cerchio
Area pentagono – Area esagono – Area ettagono
Area ottagono – Area ennagono – Area decagono
Area endecagono – Area dodecagono
Area poligoni lati regolari (3-12) – Area poligoni lati irregolari (3-10)
novità
Scopri la nuova SUITE GEOMETRIA CON VARIE WEB APP per la migliore esperienza di calcolo per ogni esigenza di Geometria!
Benvenuto nel nostro Calcolatore Area, uno strumento semplice, veloce e GRATUITO per lil calcolo di varie tipologie di aree. Che tu sia uno studente, un professionista, o un appassionato di fai-da-te, il nostro convertitore ti aiuterà a calcolare diverse tipologie di aree geometriche.
Benvenuto nel nostro Calcolatore Area, uno strumento semplice, veloce e GRATUITO per lil calcolo di varie tipologie di aree. Che tu sia uno studente, un professionista, o un appassionato di fai-da-te, il nostro convertitore ti aiuterà a calcolare diverse tipologie di aree geometriche.
Le App
ISTRUZIONI D’USO:
Per utilizzare il calcolatore, segui questi semplici passaggi:
- Seleziona la forma geometrica dal menu a tendina.
- Inserisci le misure richieste nel campo o nei campi che appariranno.
- Scegli l’unità di misura desiderata (pixel, cm, mm, pollici).
- Clicca su “Calcola Area” per ottenere il risultato.
- L’area calcolata verrà mostrata sotto il pulsante, nell’unità di misura corrispondente.
- NOTA: Se clicchi sulla “i” di fianco alle varie opzioni apparirà una breve descrizione. Per non visualizzare la descrizione ricliccare ancora sulla “i”
Vantaggi Nell’Uso del Nostro Calcolatore di aree:
- Precisione: Garantisce calcoli accurati evitando errori manuali.
- Facilità d’uso: Interfaccia intuitiva che permette a chiunque di usarlo senza difficoltà.
- Versatilità: Adatto a una vasta gamma di applicazioni, dai compiti scolastici alle attività professionali e industriali.
- Sempre disponibile: Non è necessaria alcuna installazione e puoi accedervi facilmente anche da uno smartphone, basta una connessione a Internet. Ricorda di salvare la pagina tra i tuoi PREFERITI per un accesso ancora più rapido.
Trick:
Se hai bisogno di condividere velocemente con Smartphone o Tablet il risultato con qualcuno:
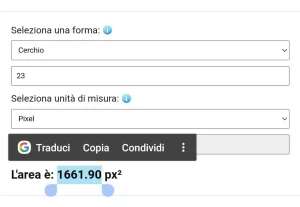
Evidenzia con il dito il risultato e poi seleziona condividi dal tuo dispositivo mobile (vedi immagine di esempio)
Nota: il tuo dispositivo potrebbe avere un aspetto differente rispetto l’immagine.
Trick:
Se hai bisogno di condividere velocemente con Smartphone o Tablet il risultato con qualcuno:
Evidenzia con il dito il risultato e poi seleziona condividi dal tuo dispositivo mobile (vedi immagine di esempio)
Nota: il tuo dispositivo potrebbe avere un aspetto differente rispetto l’immagine.

Approfondimenti
Definizione di Area:
In geometria, l’area è la misura dell’estensione di una superficie bidimensionale. Rappresenta la quantità di spazio occupato da una figura piana.
Si tratta di una grandezza che viene espressa da un numero reale non negativo. Per misurare l’area di una superficie, si confronta la sua estensione con quella di una superficie piana di riferimento, scelta come unità di misura. L’unità di misura standard per l’area nel Sistema Internazionale è il metro quadrato (m2), che corrisponde all’area di un quadrato con lato lungo 1 metro.
In termini più semplici, l’area ci dice “quanto spazio” c’è all’interno del contorno di una figura piana. Figure diverse possono avere la stessa area; in tal caso, si dicono equivalenti.
Come si calcola l’area:
Esistono diverse formule per calcolare l’area di figure geometriche specifiche, come quadrati, rettangoli, triangoli, cerchi, ecc., basate sulle dimensioni rilevanti della figura stessa. Ad esempio, l’area di un rettangolo si calcola moltiplicando la lunghezza della base per quella dell’altezza.
Il Concetto Generale di Area e la Sua Misura
Come abbiamo detto, l’area è la misura dell’estensione di una superficie piana. Immagina di voler coprire questa superficie con delle piastrelle quadrate, tutte della stessa dimensione. L’area della superficie è, concettualmente, il numero di piastrelle unitarie (cioè piastrelle che hanno un’area di 1 unità quadrata, ad esempio 1 metro quadro o 1 centimetro quadro) necessarie per coprire completamente quella superficie senza sovrapposizioni e senza lasciare spazi vuoti.
Questa idea del “riempire con quadrati unitari” è il fondamento. Tuttavia, non è pratico misurare l’area contando ogni volta i quadretti, specialmente per figure complesse o curve. Per questo motivo, la geometria ci fornisce delle formule specifiche per calcolare l’area delle figure più comuni. Queste formule derivano proprio dal concetto di base del conteggio dei quadrati unitari e dalle proprietà geometriche delle figure.
L’unità di misura dell’area è sempre un’unità di lunghezza elevata al quadrato (es. m2, cm2, km2).
Calcolo dell’Area per le Principali Figure Geometriche Piane
Ecco alcuni esempi delle formule più comuni per calcolare l’area di figure piane:
- Rettangolo:
- Concetto: È la figura più semplice da capire in termini di quadrati unitari. Se un rettangolo ha base lunga 5 unità e altezza 3 unità, puoi visualizzare 3 file di 5 quadrati unitari ciascuna.
- Formula: L’area A di un rettangolo è data dal prodotto della misura della sua base (b) per la misura della sua altezza (h). A=b×h
- Concetto: È la figura più semplice da capire in termini di quadrati unitari. Se un rettangolo ha base lunga 5 unità e altezza 3 unità, puoi visualizzare 3 file di 5 quadrati unitari ciascuna.
- Quadrato:
- Concetto: Un quadrato è un caso speciale di rettangolo in cui la base e l’altezza sono uguali (corrispondono al lato).
- Formula: L’area A di un quadrato è data dalla misura del suo lato (l) elevata al quadrato. A=l×l=l2
- Concetto: Un quadrato è un caso speciale di rettangolo in cui la base e l’altezza sono uguali (corrispondono al lato).
- Triangolo:
- Concetto: Un triangolo può essere visto come la metà di un parallelogramma (o, in casi semplici, di un rettangolo) che ha la stessa base e la stessa altezza del triangolo.
- Formula: L’area A di un triangolo è data dal semiprodotto (metà del prodotto) della misura della base (b) per la misura dell’altezza (h) relativa a quella base. A=b×h/2
- Concetto: Un triangolo può essere visto come la metà di un parallelogramma (o, in casi semplici, di un rettangolo) che ha la stessa base e la stessa altezza del triangolo.
- Parallelogramma:
- Concetto: Un parallelogramma può essere “trasformato” in un rettangolo equivalente tagliando via un triangolo da un lato e aggiungendolo sull’altro.
- Formula: L’area A di un parallelogramma è data dal prodotto della misura della base (b) per la misura dell’altezza (h) relativa a quella base. A=b×h
- Concetto: Un parallelogramma può essere “trasformato” in un rettangolo equivalente tagliando via un triangolo da un lato e aggiungendolo sull’altro.
- Trapezio:
- Concetto: Un trapezio può essere raddoppiato, ruotato e affiancato a sé stesso per formare un parallelogramma con base pari alla somma delle basi del trapezio originale e altezza pari all’altezza del trapezio. L’area del trapezio sarà quindi la metà dell’area di questo parallelogramma.
- Formula: L’area A di un trapezio è data dal semiprodotto della somma delle basi (base maggiore B e base minore b) per l’altezza (h). A=((B+b)×h)/2
- Concetto: Un trapezio può essere raddoppiato, ruotato e affiancato a sé stesso per formare un parallelogramma con base pari alla somma delle basi del trapezio originale e altezza pari all’altezza del trapezio. L’area del trapezio sarà quindi la metà dell’area di questo parallelogramma.
- Cerchio:
- Concetto: Per il cerchio (una figura curva), il concetto di “riempire con quadrati” diventa un limite. La formula si basa sul raggio (r) e sulla costante matematica π (Pi greco), che deriva dalle proprietà del cerchio stesso. Le formule per l’area del cerchio sono state scoperte con metodi che in passato prevedevano faticose approssimazioni (come il “metodo di esaustione”) e oggi si derivano con il calcolo infinitesimale.
- Formula: L’area A di un cerchio è data dal prodotto di π per il quadrato della misura del raggio (r). A=πr2
- Concetto: Per il cerchio (una figura curva), il concetto di “riempire con quadrati” diventa un limite. La formula si basa sul raggio (r) e sulla costante matematica π (Pi greco), che deriva dalle proprietà del cerchio stesso. Le formule per l’area del cerchio sono state scoperte con metodi che in passato prevedevano faticose approssimazioni (come il “metodo di esaustione”) e oggi si derivano con il calcolo infinitesimale.
Calcolo dell’Area per Figure con Contorno Irregolare (Poligoni Irregolari)
Quando una figura piana ha un contorno che non corrisponde a una delle forme geometriche standard (ad esempio, un poligono con molti lati di lunghezze diverse e angoli variabili), non esiste un’unica formula semplice. In questi casi, si possono usare diverse strategie:
- Decomposizione: Si cerca di dividere la figura irregolare in figure geometriche più semplici di cui conosciamo le formule (triangoli, quadrati, rettangoli, trapezi, ecc.). Si calcola l’area di ciascuna di queste figure più semplici e poi si sommano tutte le aree parziali per ottenere l’area totale della figura irregolare.
- Esempio Concettuale: Immagina una figura a forma di “L”. Puoi dividerla in due rettangoli (uno verticale e uno orizzontale). Calcoli l’area dei due rettangoli separatamente e poi le sommi. Lo stesso principio si applica a poligoni con più lati.
- Esempio Concettuale: Immagina una figura a forma di “L”. Puoi dividerla in due rettangoli (uno verticale e uno orizzontale). Calcoli l’area dei due rettangoli separatamente e poi le sommi. Lo stesso principio si applica a poligoni con più lati.
- Metodo del Reticolo (Approssimazione): Se la figura è disegnata su carta quadrettata, si può stimare l’area contando i quadrati unitari completamente interni alla figura e sommando a metà il numero dei quadrati che sono attraversati dal bordo della figura. Questo metodo è un’approssimazione, più precisa quanto più piccoli sono i quadrati del reticolo.
- Formule basate sulle Coordinate (per Poligoni Irregolari): Se i vertici del poligono irregolare sono noti tramite le loro coordinate cartesiane (xi,yi), esiste una formula specifica (spesso chiamata “formula dell’area di Gauss” o “formula del laccio”) che permette di calcolare l’area in modo
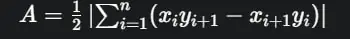
- dove n è il numero di vertici, (xi,yi) sono le coordinate dell’i-esimo vertice, e per i=n, (xn+1,yn+1) sono le coordinate del primo vertice (x1,y1). Il valore assoluto serve a garantire che l’area sia positiva.
Riguardo alle “Figure con Più Facce Irregolari”
Se con “figura geometrica con più facce N irregolari” intendi un solido geometrico (una figura tridimensionale) le cui superfici esterne sono irregolari, allora non stai calcolando l’area piana, ma la superficie totale del solido. In questo caso, il principio generale è simile alla decomposizione per le figure piane irregolari:
- Identifica tutte le facce (le superfici piane che delimitano il solido).
- Per ogni faccia, determina la sua forma e calcola la sua area usando il metodo più appropriato per quella specifica forma piana (potrebbe essere una delle formule standard o richiedere la decomposizione se la faccia è un poligono irregolare).
- Una volta calcolata l’area di tutte le facce, somma queste aree parziali per ottenere l’area della superficie totale del solido.
In sintesi, calcolare l’area significa quantificare lo spazio bidimensionale occupato da una figura. Per le forme comuni si usano formule specifiche derivate dal concetto di riempimento con unità quadrate. Per le forme più complesse o irregolari, si ricorre alla scomposizione in figure più semplici o a metodi basati sulle coordinate o sull’approssimazione. Per i solidi, si calcola l’area di ogni faccia e si somma.
Applicazioni dell”Area in Diversi Contesti
Il nostro calcolatore di aree è uno strumento versatile che può essere utile in molteplici contesti, tra cui:
- Educazione: Studenti e insegnanti possono utilizzarlo per calcolare rapidamente le aree durante le lezioni di geometria.
- Architettura e Ingegneria: Professionisti possono determinare le aree di vari spazi e componenti strutturali.
- Design e Arredamento: Designer di interni e arredatori possono calcolare l’area di stanze e superfici per la pianificazione degli spazi.
- Progetti Fai-da-te: Appassionati di bricolage possono usarlo per pianificare la quantità di materiali necessari per i loro progetti.
- Arte e Artigianato: Artisti e artigiani possono determinare le dimensioni delle superfici di lavoro per le loro opere.
